Scientific work
Systems with symmetries
For a long period of time I have been involved in the study of Hamiltonian
dynamical systems with symmetries of different kinds. Such systems are very
common in atomic and molecular physics. (In fact it is diffiult to come up with
a molecular or atomic system which has no symmetry.) One of the problems
arising in this study is the analysis of group actions on manifolds.
As an example consider the study of the action of the tetrahedral group
Td on the complex projective space CP
2 made by Boris
Zhilinskií in 1985
[
Chem. Phys. 137, 1 (1989)]
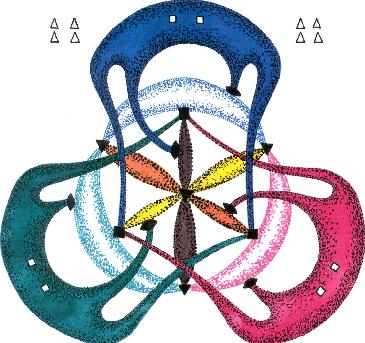
Incredible as it may seem, this old abstract work by Boris has recently
found direct applications in molecules
[
Dhont-2000,
VanHecke-2001].
In fact, molecular vibrations about the equilibrium configuration can be
described using a normalized system, whose principal or
polyad
integral
n is (approximately) the linear part of the vibrational
Hamiltonian. This
n is quite similar to the principal quantum number of
the hydrogen atom. In molecules,
n is a good quantum number which labels
polyads (aka
n shells).
The space CP
2 is a reduced phase space of the 3-oscillator system,
which is described in the lowest approximation as an isotropic 1:1:1 resonant
harmonic oscillator. In the case of the triply degenerate vibrational
F modes of molecules with cubic (
Td or
Oh) equilibrium configuration [
Efstathiou-2004], such resonance is
exact; in some other cases, such as ozone molecule
[
Kozin-2004], it is
approximate. In both cases, we consider and reduce the approximate dynamical
(or polyad) symmetry
S1 generated by the flow of the linear 3-mode system in 1:1:1
resonance.
 Knowing the group action, we can predict qualitatively the types of Hamiltonian
functions compatible with given symmetry and topology of the manifold (phase
space) on which these functions are defined. A classic example of such
prediction is the reduced rotational Hamiltonian of the spherical top molecule
defined on a 2-sphere in the presence of the
Oh symmetry, see on the left.
Knowing the group action, we can predict qualitatively the types of Hamiltonian
functions compatible with given symmetry and topology of the manifold (phase
space) on which these functions are defined. A classic example of such
prediction is the reduced rotational Hamiltonian of the spherical top molecule
defined on a 2-sphere in the presence of the
Oh symmetry, see on the left.
Analysis of quantum rotational states usung symmetries of the classical limit
effective rotational Hamiltonian goes back to the work
of J.K.G.Watson. In the 1980, it was widely popularized
by W.Harter and was extended by my teacher and frequent
co-author Boris Zhilinskií. So Boris and his co-worker Igor
Pavlichenkov predicted an interesting dynamical phenomenon: when under
increasing rotational excitation and increasing centrifugal distortion the
normally asymmetric top molecule AB2 becomes accidentally symmetric,
one of its stable stationary axes of rotation (the axis of the principal
inertia tensor of the equilibrium configuration) goes unstable and two
new equivalent stable axes become created. The quantum consequence of this
bifurcation is the formation of 4-fold quasi-degenerate groups (clusters) of
rotational states in addition to/in place of “usual” for asymmetric
tops doublets. This was observed in heavy-central-atom molecules, such as
H2Se in the 1990.

The DMSO saga (2010-2013)
More recently, while the subject of rotational clusters was firmly entering
modern textbooks on rotational structure of molecules, we made a comeback to
this field by uncovering essentially the same phenomenon but in a
polyatomic
molecule DMSO [
Cuisset-2012]. The story began at
our lab Christmas party in 2009, when my colleague
Arnaud Cuisset asked
me, as a theoretician, to help with an unusually dense (for an asymmetric top)
high resolution vibration-rotation spectrum of DMSO
[
Cuisset-2013], which he observed
together with
Olivier Pirali using the synchrotron beam source.
Indeed, from a look of it, one would think of a spherical top... The spectral
density (and difficulty) is due both to the small rotational constants of this
relatively heavy molecule and the accidental closeness of its equilibrium
configuration to that of the symmetric top. The latter fact already rang some
bells...
Months of a very intense work, requiring the state-of-the-art analysis of
thousands of spectroscopic lines followed. It turned out that certain skills,
like riding a bicycle or skiing, stay with us longer than we think. After
almost 20 years, I had to recall all what I learned and used while working in
the Spectroscopy section of the Herzberg Institute of Astrophysics in Ottawa
(
see below).
After succeeding in understanding the ν
11 transition
[
Cuisset-2010], we turned to the even more
intriguing ν
23 band.
A good surprize awaited us there[
Cuisset-2012]: the recovered
rotational structure of the vibrational state ν
23 of DMSO
suggested clearly the pitchfork bifurcation, in which the high-energy
stationary axis of rotation looses stability and two new equivalent stable axes
get created at angular momenta
J larger than 50 (see the
animated rotational energy surface of ν23, top left). We
called this remarkable phenomenon
gyroscopic destabilization, and we
were able to attribute a number of spectroscopic transitions in this band to
the 4-fold clusters (of localized states) representing rotation about the newly
created axes. So the scientific heritage of
Boris Zhilinskií, who
followed our work with great interest, has been put to work yet again.
Spectroscopy
My PhD thesis was in part dealing with the analysis and assignment of
experimental high-resolution rotation-vibration spectra of spherical top
molecules. Together with Volodya Krivtsun, we were one of the first
to observe the ν3 band of the rare SnH4
molecule.
 Later, at the Herzberg Institute in Ottawa in 1990-93, I worked with Izabel
Dabrowski and late Gerhard Herzberg (right) on the spectra of
Rydberg molecules ArD and KrD. A combination of Izabel's expertise in the art
of line assignments, my postdoc freshness, GH's inspiration and persistence,
encouragement by John W. C. Johns, and, of course, a bit of luck, led
to our first successful assignment and analysis of spectra of these molecules
which had been puzzling people since they were first seen more than 10 years
before us. The work on ArD was probably the last research work in which GH
truly participated. When I remember this work, I always imagine him the way he
is shown in the photo, coming into my office with suggestions and more spectra.
These suggestions turned out to be very important indeed. To have an idea of
the complexity of the spectra we worked with, see the example of the
4f(complex)→4d(Δ) band below.
Later, at the Herzberg Institute in Ottawa in 1990-93, I worked with Izabel
Dabrowski and late Gerhard Herzberg (right) on the spectra of
Rydberg molecules ArD and KrD. A combination of Izabel's expertise in the art
of line assignments, my postdoc freshness, GH's inspiration and persistence,
encouragement by John W. C. Johns, and, of course, a bit of luck, led
to our first successful assignment and analysis of spectra of these molecules
which had been puzzling people since they were first seen more than 10 years
before us. The work on ArD was probably the last research work in which GH
truly participated. When I remember this work, I always imagine him the way he
is shown in the photo, coming into my office with suggestions and more spectra.
These suggestions turned out to be very important indeed. To have an idea of
the complexity of the spectra we worked with, see the example of the
4f(complex)→4d(Δ) band below.
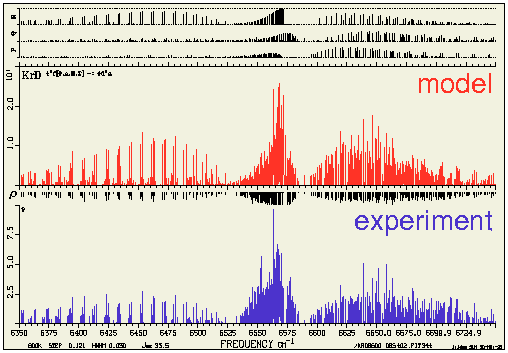 Several such bands are usually needed in order to extract information on the
rotational structure of the participating electronic Rydberg states.
After leaving Ottawa, I had little opportunity to work with actual
spectroscopic data, even though I always liked the feeling of working with real
systems. Some people, to whom I told of my past experiences in molecular
spectroscopy, would ask «Why are you people still doing this? To convince
that quantum mechanics is right?». My own scientific interests and work
grew more mathematical. Yet, many years later, together with Arnaud
Cuisset, I became deeply involved in the analysis of his experimental
spectroscopic data on
DMSO. This was the most successful collaboration with the
experimenters in our lab in Dunkerque.
Several such bands are usually needed in order to extract information on the
rotational structure of the participating electronic Rydberg states.
After leaving Ottawa, I had little opportunity to work with actual
spectroscopic data, even though I always liked the feeling of working with real
systems. Some people, to whom I told of my past experiences in molecular
spectroscopy, would ask «Why are you people still doing this? To convince
that quantum mechanics is right?». My own scientific interests and work
grew more mathematical. Yet, many years later, together with Arnaud
Cuisset, I became deeply involved in the analysis of his experimental
spectroscopic data on
DMSO. This was the most successful collaboration with the
experimenters in our lab in Dunkerque.
Normal forms
As a postdoc with John Delos in
1993-94, I worked on the normal form study of periodic orbits. Although the
theory of normalization near periodic orbits existed at the time, there were no
serious numerical practical applications of it before us. One of the systems
studied in John's group was hydrogen atom in external crossed magnetic and
electric fields. John was interested in bifurcations basic periodic orbits
(=relative equilibria) of this system. We computed normal forms near one
particular orbit, the so-called ``perpendicular'' orbit.
This is how our normal form worked.
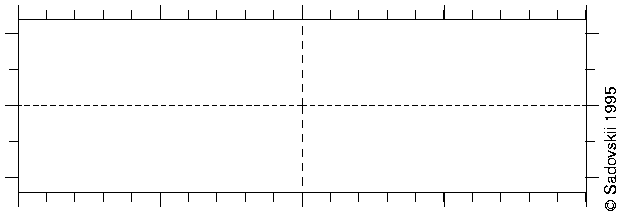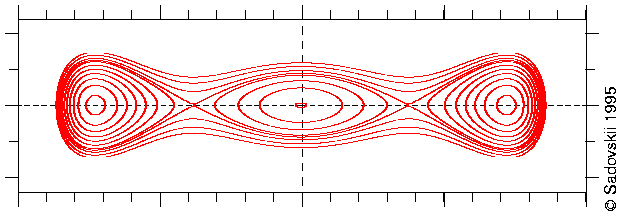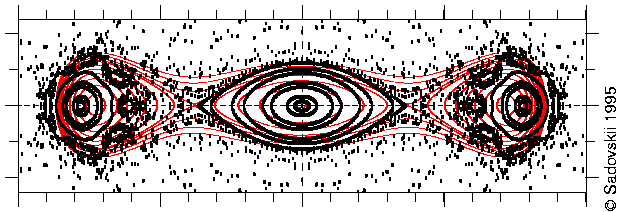
Here black dots show the Poincaré surface of section computed by
John
Shaw, red shows constant level sets of the normalized Hamiltonian. The
pair of Z
2-symmetric pairs of stable-unstable satellite orbits was
created just before in a fold bifurcation, and now the two unstable orbits move
tovards centre as the energy increases. The perpendicular orbit in the centre
is about to have a period-1 Z
2-symmetric bifurcation and loose
stability. The normal form describes well this ``organized'' sequence of
bifurcations [
SadovskiiDelos-95]. The two small stable
islands correspond to the two new periodic orbits which branched off for good.
Secondary high-period resonances, which mark the onset of chaos, can be seen
around these islands.
Relative equilibria
My work is related in many ways to the study of relative equilibria
(RE), including those of vibrating and rotating molecules, and of the perturbed
Kepler problem and its quantum analogue, the hydrogen atom in external fields.
RE are special periodic orbits of the system which go along the orbit of the
group action of a dynamical or strict symmetry group. In all systems we
studied, we have the S1 group action.
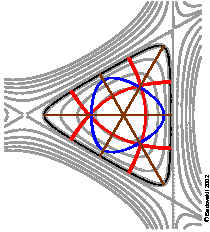
A simple comprehensive explanation of what RE are and how we use them can be
given using the ``textbook''
Hénon-Heiles system [
DS:SPT2001], which has close micro
analogues, such as the
E-mode vibrations of H
3+
[
SFHTZ-1993] or P
4 and other molecules with
cubic symmetry. The Hénon-Heiles system is a 1:1 resonant 2-oscillator
with the anharmonic
D3 symmetric potential
V(x,y)
shown left. Near the central equilibrium
(0,0), we have eight RE or
nonlinear normal modes, whose projections on the coordinate plane are
shown on top of
V(x,y).
Among the eight RE, two stable equivalent circular RE retain
C3 symmetry and share the same
(x,y) image (blue loop)
but differ in direction. Six other
C2 symmetric RE bounce at
the potential energy limit (black) : three stable equivalent RE lie in the
symmetry planes (straight red lines), while three remaining RE are unstable.
Perturbed Keplerian systems
Perturbations of the hydrogen atom by external fields are atomic analogues of
classical perturbed Kepler systems. I started to work in this field as a
postdoc with John Delos. We normalized near the perpendiqular RE (one
of the four basic periodic orbits or Kepler ellipses) of the crossed fields
system (hydrogen atom perturbed by orthogonal electric and magnetic fields) and
studied bifurcations of this periodic orbit.
Later with Boris Zhilinskií we studied normal forms near the
equilibrium of the regularized Kepler system. We applied invariant theory and
studied the topology of the reduced spaces and orbit spaces. Together with
Boris and Louis Michel we uncovered and interpreted the phenomenon of
crossover.
My experience with these systems was a key to the successful collaboration with
Richard Cushman on the monodromy of the
hydrogen atom in crossed fields.
Monodromy
More recently, I worked with Richard Cushman, who introduced me and
Boris to the idea of monodromy, or basic topological obstuction to the
existence of global action-angle variables in classical Hamiltonian dynamical
systems. In this sense, monodromy was introduced by J. J. Duistermaat in 1980.
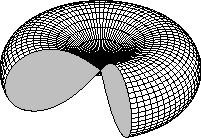
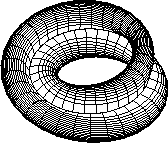
In the simplest case of a classical mechanical integrable Hamiltonian system
with two degrees of freedom, monodromy exists if one of the singular
dynamically invariant subspaces of the system is an isolated fiber, which
Cushman called
pinched torus (see left). It can be represented as a
2-torus with one basis cycle contracted to a point. The latter corresponds to
the unstable equilibrium of the
focus-focus type; the rest of this
fiber is the stable and unstable manifolds of the equilibrium forming a
homoclinic connection. In systems with parameters, appearance of such
focus-focus points and their symmetric variations results from
Hamiltonian
Hopf bifurcations.
We studied the quantum analogues of systems with monodromy. Boris proposed to
manifest quantum monodromy as a point defect in the lattice of quantum
states in the joint energy-momentum spectrum.
One of the most fundamental systems
with monodromy, which we found with Richard [CushmanSadovskii-1999, CushmanSadovskii-2000], is the
hydrogen atom in orthogonal (or crossed) external electric and magnetic
fields. The energy-momentum diagram of this system for two different relative
field strengths is shown below.
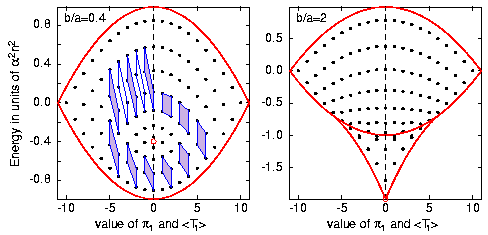 On the left, the system has monodromy. The absence of globally defined quantum
numbers is illustrated by "Zhilinskií's defect diagram". Take the elementary
cell of the lattice, move it along a countour around the isolated critical
(singular) value of the energy-momentum map indicated by the red circle, and
compare the initial and final cells. The cells don't match!
On the left, the system has monodromy. The absence of globally defined quantum
numbers is illustrated by "Zhilinskií's defect diagram". Take the elementary
cell of the lattice, move it along a countour around the isolated critical
(singular) value of the energy-momentum map indicated by the red circle, and
compare the initial and final cells. The cells don't match!
Monodromy of floppy triatomic molecules
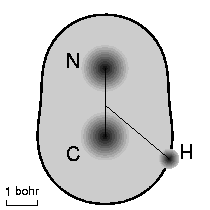
Finding monodromy in real systems may not be all that easy, as we learned with
Marc Joyeux
in 2003. We had many good reasons to believe that the bending
vibrational system of the isomerizing HCN/CNH molecule should have
monodromy. To understand this system, I came up with a nice model system, a
, which does have monodromy.
However, when we tried the same analysis for the real case of HCN/CNH, we found
that the segment of singular values
(the upper boundary of the green leaf) became unbounded, see figure below.
So, instead, we have suggested that the HCN/CNH system has the
generalized two-branch global bending quantum number
.
Later Marc applied the same analysis to LiNC/NCLi
[JST-2003]
and it worked
.
The reason for such difference between HCN/CNH and
LiNC/NCLi is the "shape" of the system: in HCN/CNH, the H atom moves on a
peanut-like surface with a waist, for as the much larger Li atom cannot
get too close to the CN diatom and the shape of LiNC/NCLi remains convex.
Fractional monodromy
As Boris continued to study various defects of ``quantum lattices´´, he came to
the idea of fractional monodromy, a generalization of the monodromy
phenomenon. He suggested that fractional monodromy corresponds to a linear
defect caused by the line of ``weak'' singular values in the base of the
integrable foliation. In our joint work with Nikolaí Nekhoroshev
we gave rigorous mathematical
definition of fractional monodromy and computed it on the example of the
classical 1:-2 resonant nonlinear oscillator [NSZ-2002]. The corresponding
energy-momentum diagram is shown below. 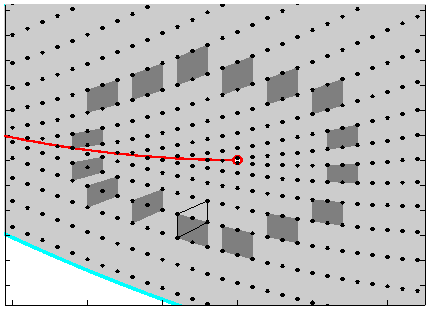 It can be easily seen that we can only use a double elementary cell to
cross the line of weak singularities shown in red, and that the monodromy
matrix of the transformation of the single cell has a half-integer element.
It can be easily seen that we can only use a double elementary cell to
cross the line of weak singularities shown in red, and that the monodromy
matrix of the transformation of the single cell has a half-integer element.
The underlying singularity of the corresponding classical 1:-2 resonant system
is due to the presence of special “short” orbits of the oscillator
action S
1, whose period is half that of the regular S
1
orbits. Dynamically these orbits correspond to the pure excitation of the
second oscillator and due to the nonlinear resonance terms they are unstable.
The stable and unstable manifolds conect and form a 2D singular variety, which
we call a
curled torus, shown left. In fact, points of the red line
in the above energy-momentum diagram are images of such tori.
To compute monodromy, we consider a bundle over the closed contour Γ,
which goes around the central singular point (red circle) in the image of the
energy-momentum map. Since Γ has to cross the singular (red) line, this
bundle has one singular fiber---the curled torus. To compute monodromy, we
identifiy continuously the fundamental groups π
1 of the regular
fibers (tori) in the bundle while we move along Γ.
According to Nekhoroshev, we cannot continue the whole π
1 when we
cross the singular line, but we
can continue a complete
subgroup ζ of π
1. What exactly happens to the
basis cycles of π
1 can be well represented
on the
.
After making one tour on Γ, we obtain the final subgroup ζ(1) and
compare it to the original subgroup ζ(0), with which we started our tour.
The map ζ(1)→ζ(0) is nontrivial. When formally extended to the
whole π
1, the matrix for this map has rational coefficients
(½ in the case of the 1:-2 resonance). Hence the term
fractional.
It is intresting to note that as a graduate student of Vl. I. Arnold in the
late 60s, Nikolaí formulated the necessary condititions for the existence of
global action-angle variables, i.e., for the absence of monodromy, see his
Two theorems about action-angle variables, Uspekhi
Mat. Nauk 24 no 5 (1969) 237-238 (in Russian); Russian Math. Surveys
24 no 5 (1969) 237-38. So after 30 years Nikolaí comes back in
the field with another fundamental contribution!


 Knowing the group action, we can predict qualitatively the types of Hamiltonian
functions compatible with given symmetry and topology of the manifold (phase
space) on which these functions are defined. A classic example of such
prediction is the reduced rotational Hamiltonian of the spherical top molecule
defined on a 2-sphere in the presence of the
Oh symmetry, see on the left.
Knowing the group action, we can predict qualitatively the types of Hamiltonian
functions compatible with given symmetry and topology of the manifold (phase
space) on which these functions are defined. A classic example of such
prediction is the reduced rotational Hamiltonian of the spherical top molecule
defined on a 2-sphere in the presence of the
Oh symmetry, see on the left.



 A simple comprehensive explanation of what RE are and how we use them can be
given using the ``textbook'' Hénon-Heiles system [DS:SPT2001], which has close micro
analogues, such as the E-mode vibrations of H3+
[SFHTZ-1993] or P4 and other molecules with
cubic symmetry. The Hénon-Heiles system is a 1:1 resonant 2-oscillator
with the anharmonic D3 symmetric potential V(x,y)
shown left. Near the central equilibrium (0,0), we have eight RE or
nonlinear normal modes, whose projections on the coordinate plane are
shown on top of V(x,y).
Among the eight RE, two stable equivalent circular RE retain
C3 symmetry and share the same (x,y) image (blue loop)
but differ in direction. Six other C2 symmetric RE bounce at
the potential energy limit (black) : three stable equivalent RE lie in the
symmetry planes (straight red lines), while three remaining RE are unstable.
A simple comprehensive explanation of what RE are and how we use them can be
given using the ``textbook'' Hénon-Heiles system [DS:SPT2001], which has close micro
analogues, such as the E-mode vibrations of H3+
[SFHTZ-1993] or P4 and other molecules with
cubic symmetry. The Hénon-Heiles system is a 1:1 resonant 2-oscillator
with the anharmonic D3 symmetric potential V(x,y)
shown left. Near the central equilibrium (0,0), we have eight RE or
nonlinear normal modes, whose projections on the coordinate plane are
shown on top of V(x,y).
Among the eight RE, two stable equivalent circular RE retain
C3 symmetry and share the same (x,y) image (blue loop)
but differ in direction. Six other C2 symmetric RE bounce at
the potential energy limit (black) : three stable equivalent RE lie in the
symmetry planes (straight red lines), while three remaining RE are unstable.
 In the simplest case of a classical mechanical integrable Hamiltonian system
with two degrees of freedom, monodromy exists if one of the singular
dynamically invariant subspaces of the system is an isolated fiber, which
Cushman called pinched torus (see left). It can be represented as a
2-torus with one basis cycle contracted to a point. The latter corresponds to
the unstable equilibrium of the focus-focus type; the rest of this
fiber is the stable and unstable manifolds of the equilibrium forming a
homoclinic connection. In systems with parameters, appearance of such
focus-focus points and their symmetric variations results from Hamiltonian
Hopf bifurcations.
In the simplest case of a classical mechanical integrable Hamiltonian system
with two degrees of freedom, monodromy exists if one of the singular
dynamically invariant subspaces of the system is an isolated fiber, which
Cushman called pinched torus (see left). It can be represented as a
2-torus with one basis cycle contracted to a point. The latter corresponds to
the unstable equilibrium of the focus-focus type; the rest of this
fiber is the stable and unstable manifolds of the equilibrium forming a
homoclinic connection. In systems with parameters, appearance of such
focus-focus points and their symmetric variations results from Hamiltonian
Hopf bifurcations.

 Finding monodromy in real systems may not be all that easy, as we learned with
Marc Joyeux
in 2003. We had many good reasons to believe that the bending
vibrational system of the isomerizing HCN/CNH molecule should have
monodromy. To understand this system, I came up with a nice model system, a
, which does have monodromy.
However, when we tried the same analysis for the real case of HCN/CNH, we found
that the segment of singular values
(the upper boundary of the green leaf) became unbounded, see figure below.
So, instead, we have suggested that the HCN/CNH system has the
generalized two-branch global bending quantum number
.
Later Marc applied the same analysis to LiNC/NCLi
[JST-2003]
and it worked
.
The reason for such difference between HCN/CNH and
LiNC/NCLi is the "shape" of the system: in HCN/CNH, the H atom moves on a
peanut-like surface with a waist, for as the much larger Li atom cannot
get too close to the CN diatom and the shape of LiNC/NCLi remains convex.
Finding monodromy in real systems may not be all that easy, as we learned with
Marc Joyeux
in 2003. We had many good reasons to believe that the bending
vibrational system of the isomerizing HCN/CNH molecule should have
monodromy. To understand this system, I came up with a nice model system, a
, which does have monodromy.
However, when we tried the same analysis for the real case of HCN/CNH, we found
that the segment of singular values
(the upper boundary of the green leaf) became unbounded, see figure below.
So, instead, we have suggested that the HCN/CNH system has the
generalized two-branch global bending quantum number
.
Later Marc applied the same analysis to LiNC/NCLi
[JST-2003]
and it worked
.
The reason for such difference between HCN/CNH and
LiNC/NCLi is the "shape" of the system: in HCN/CNH, the H atom moves on a
peanut-like surface with a waist, for as the much larger Li atom cannot
get too close to the CN diatom and the shape of LiNC/NCLi remains convex.

 The underlying singularity of the corresponding classical 1:-2 resonant system
is due to the presence of special “short” orbits of the oscillator
action S1, whose period is half that of the regular S1
orbits. Dynamically these orbits correspond to the pure excitation of the
second oscillator and due to the nonlinear resonance terms they are unstable.
The stable and unstable manifolds conect and form a 2D singular variety, which
we call a curled torus, shown left. In fact, points of the red line
in the above energy-momentum diagram are images of such tori.
To compute monodromy, we consider a bundle over the closed contour Γ,
which goes around the central singular point (red circle) in the image of the
energy-momentum map. Since Γ has to cross the singular (red) line, this
bundle has one singular fiber---the curled torus. To compute monodromy, we
identifiy continuously the fundamental groups π1 of the regular
fibers (tori) in the bundle while we move along Γ.
According to Nekhoroshev, we cannot continue the whole π1 when we
cross the singular line, but we can continue a complete
subgroup ζ of π1. What exactly happens to the
basis cycles of π1 can be well represented
on the
.
After making one tour on Γ, we obtain the final subgroup ζ(1) and
compare it to the original subgroup ζ(0), with which we started our tour.
The map ζ(1)→ζ(0) is nontrivial. When formally extended to the
whole π1, the matrix for this map has rational coefficients
(½ in the case of the 1:-2 resonance). Hence the term
fractional.
The underlying singularity of the corresponding classical 1:-2 resonant system
is due to the presence of special “short” orbits of the oscillator
action S1, whose period is half that of the regular S1
orbits. Dynamically these orbits correspond to the pure excitation of the
second oscillator and due to the nonlinear resonance terms they are unstable.
The stable and unstable manifolds conect and form a 2D singular variety, which
we call a curled torus, shown left. In fact, points of the red line
in the above energy-momentum diagram are images of such tori.
To compute monodromy, we consider a bundle over the closed contour Γ,
which goes around the central singular point (red circle) in the image of the
energy-momentum map. Since Γ has to cross the singular (red) line, this
bundle has one singular fiber---the curled torus. To compute monodromy, we
identifiy continuously the fundamental groups π1 of the regular
fibers (tori) in the bundle while we move along Γ.
According to Nekhoroshev, we cannot continue the whole π1 when we
cross the singular line, but we can continue a complete
subgroup ζ of π1. What exactly happens to the
basis cycles of π1 can be well represented
on the
.
After making one tour on Γ, we obtain the final subgroup ζ(1) and
compare it to the original subgroup ζ(0), with which we started our tour.
The map ζ(1)→ζ(0) is nontrivial. When formally extended to the
whole π1, the matrix for this map has rational coefficients
(½ in the case of the 1:-2 resonance). Hence the term
fractional.